To compute the 2-d Fourier Transform of a matrix, use the fft2d command.
- fft2d2d fast Fourier transform
-
matrix -- or a list {real part, imaginary part} of 2 matrices
[inverse] boolean -- default false, if true the inverse fft
-
Result: matrix -- {real part, imaginary part} of the resulting fft.
The example below computes and displays the 2-d Fourier transform for an interference pattern obtained with three red lasers. To view the original image (a TIFF file) in a new window, click here. Then drop the picture to your desktop to download the .tiff file.
The example assumes that the file was downloaded to your desktop. Otherwise, edit the first line.
|
Import script
set f to ((path to desktop as text) & "V_3H_1.tiff") as alias
set r to imagefile bounds f
set m to convert imagefile f selected rectangle {0, 0, 256, 256}
set nc to ncols of m
set nr to nrows of m
set av to mean of (statlist m)
set a to sublist array of real of m with av
-- the lines below force the null value on the boundaries
set x to creatematrix "x" ncols nc nrows nr
set y to creatematrix "y" ncols nc nrows nr
set the_formula to "sin(pi*x/nc)*sin(pi*y/nr)*a"
set array of real of m to evalformula the_formula with {a:a, x:x, y:y, nc:nc, nr:nr}
set sm to DoQuickFFT(m, 0, 0)
set sm's color palette to "GrayInv"
set v to sm's container
set v's limits to {-50, 50, -50, 50}
draw v
|
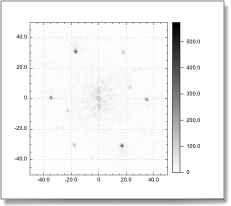
The 2-d spectrum of an image obtained in a laser interference experiment
|