• To compute the 1-d Fourier Transform of an array of real, use the short form of the fft1d command.

  fft1dNormalized fast Fourier transform.

  array of real -- or a list {real part, imaginary part} of 2 arrays of real
  [inverse] boolean -- default false, if true the inverse fft

  Result: array of real -- {real part, imaginary part} of the resulting fft.

  fft1d lets you compute the Fourier Transform for an array of real numbers or for an array of complex numbers. In the latter case, provide the real part and the imaginary part as a list of two arrays of real.
• To compute a general, grouped, N-dimensional Fourier Transform of vectors, use the advanced form of the fft1d command.

  fft1dThe general interface for grouped and n-dimensional fft.

  array of real -- or a list {real part, imaginary part} of 2 arrays of real
  [inverse] boolean -- default false, if true the inverse fft
  [lot] integer -- the number of vectors to transform
  [vector size] integer -- the number of elements of each vector
  [vector step] integer -- the distance between elements in a vector
  [vector offset] integer -- the distance between vectors

  Result: array of real -- {real part, imaginary part} of the resulting fft.

• The execution time of fft1d is of order N.Log(N), whatever the sizes of the arrays. However, fft1d is faster when the size of the vectors is the product of powers of small prime numbers.

Import script

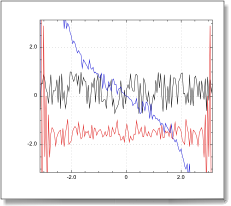
set x to createarray 144 range {-pi, pi}
set y to randomarray 144 range {-0.75, 1}
set ys to runningsum y
set c to QuickCurve(x, y, 0)
set v to c's container
set {kr, ki} to fft1d ys
QuickCurve(x, kr, v)
QuickCurve(x, ki, v)
set v's limits to {-pi, pi, -pi, pi}
draw v